| Trần Hải Nam – 2201040119 | Nguyễn Thị Hạ Vy – 2301040204 |
| Phan Thuỳ Ngân – 2201040126 | Phùng Đinh Linh Ngân – 2201040127 |
| Nguyễn Ngọc Lan – 2201040093 | Nguyễn Thị Thuỷ Chung – 2201040024 |
| Nguyễn Thị Tuyết – 2201040163 | Nguyễn Thị Mai Phương – 2201040142 |
ABSTRACT
Middle East geopolitical conflicts have led to a profound refugee crisis, leaving millions to languish in overcrowded encampments while provinces grapple with a disparate distribution of displaced persons. This imbalance places undue strain on infrastructure, exacerbates social tensions, and heightens security concerns, emphasizing the urgent need for a carefully designed resettlement strategy. To tackle this issue, Stable matching theory (SMT) was applied as a mathematical framework to find efficient and stable pairings between refugees and host provinces, optimizing mutual satisfaction and fostering long-term sustainability. Beyond optimizing refugee allocation, the research outcomes underpin national policy reforms, address complex social challenges, and foster multi-stakeholder collaboration. Specifically, our study proposes an integrated approach leveraging the Gale-Shapley algorithm (GSA) within the SMT framework and enhancing it through OMOPSO – a multi-objective optimization technique. Building upon this foundation, the approach supports stable matching under multiple constraints by GSA, and achieves fair refugee distribution across provinces due to OMOPSO balancing multi-objective criteria such as life quality, health, and financial.
Keywords: Stable matching theory, Gale-Shapley algorithm, OMOPSO algorithm, refugee relocation, efficient allocation.
I. Introduction
1.1. Background
The uneven distribution of refugees within host countries like Jordan and Lebanon has led to severe socio-economic challenges, straining infrastructure, public services, and social cohesion in provinces hosting refugees. In Jordan, urban centers such as Amman, Irbid, and Mafraq collectively host over 70% of refugees, while in Lebanon, the Beqaa Valley alone accommodates around 36.1%, creating regional disparities [1], [2]. Overcrowded schools in these areas operate on double shifts, reducing education quality, while healthcare systems struggle to meet rising demands. These pressures exacerbate tensions between locals and refugees, as international aid often prioritizes the latter, fueling social divides [3]. Beyond the Middle East, the crisis has affected Europe, where the EU introduced the European Agenda on Migration to manage asylum seekers through measures like the “hotspot” approach and emergency relocation plans. However, opposition from member states led to the failure of the relocation scheme, sparking legal disputes and limiting the Agenda’s effectiveness [4].
Figure 1: Distribution of refugees in Jordan provinces
The refugee crisis has become a complex issue, with challenges including the uneven distribution of refugees and inadequate integration policies. According to the World Bank, this strain overwhelms border regions and urban centers, leading to overcrowded facilities and overburdened healthcare systems [5]. In Lebanon, major cities face the most pressure, while other areas with available capacity remain underused. Figure 2 illustrates the shift in health expenditure, with government spending rising from 43% in 2012 to 45% in 2017, while out-of-pocket expenses fell from 37% to 33%. In high refugee-density areas, the growing demand for medical services intensifies these financial pressures, raising concerns about equitable and sustainable healthcare access for both host populations and refugees [6].
Figure 2: Sources of Lebanese health expenditure (%)
This led to logistical challenges and social tensions between refugees and local communities. The inadequacy of short-term integration policies, like temporary shelters, underscored the need for long-term solutions addressing refugees’ ongoing needs in education and employment [7]. Aligning refugee relief with sustainable integration policies is crucial to balance resources, reduce tensions, and enable refugees to contribute meaningfully to host provinces.
SMT provides a theoretically sound and practically efficient framework for solving complex allocation problems such as refugee resettlement. It ensures mutually beneficial and conflict-free matching based on preference rankings [8]. Developed by Lloyd Shapley and applied by Alvin Roth to real-world scenarios like organ donation and school choice, the work earned them the Nobel Prize in 2012 and has proven to be widely applicable [9]. A key component of SMT is the Gale-Shapley algorithm, which achieves stable matchings by having one group propose to the other based on their preferences, with proposals being accepted or rejected iteratively until a stable arrangement is reached [10]. Teytelboym emphasizes that this mechanism is particularly suitable for refugee allocation because it balances refugee needs with local preferences and capacity constraints, thereby reducing the likelihood of conflicts [11]. To further improve allocation outcomes, we integrate SMT with multi-objective evolutionary algorithms such as OMOPSO, which allow for the simultaneous optimization of multiple fairness and efficiency criteria.
To enhance refugee allocation efficiency, Multi-Objective Evolutionary Algorithms (MOEAs) are employed for their ability to optimize conflicting objectives and generate a Pareto approximation set in a single run for multi-objective problems (MOPs) [12]. Among them, Particle Swarm Optimization (PSO) is recognized for effectively exploring the search space by generating a densely distributed solution population through its arithmetic mechanism [13]. A notable PSO-based MOEA is OMOPSO [14], which pioneered the use of ɛ-dominance in many-objective optimization, improving its ability to handle high-dimensional decision-making.
Figure 3. Average GD to the Pareto’s ideal front by each algorithm [17]
As shown in Figure 3, OMOPSO achieves the smallest Generational Distance (GD) to the Pareto ideal front, indicating its strong convergence capability in refugee allocation tasks. This confirms its effectiveness in producing solutions close to the true Pareto front. OMOPSO successfully balances conflicting objectives such as economic viability, social integration, and humanitarian needs [15]. Its optimization superiority over other algorithms has been validated in several studies [16]. Thus, OMOPSO emerges as a reliable and practical tool for supporting decisions in refugee allocation, offering optimal trade-offs between competing factors in complex real-world scenarios [17].
1.2. Related work
This section examines major research on refugee distribution processes and integration techniques in various locations, including Europe and the Middle East. It emphasizes the development of approaches for successful refugee allocation that not only consider preferences and capabilities but also promote long-term integration and well-being. Additionally, the review identifies gaps in current models, highlighting the need for more effective solutions. As a result, this study aims to provide improved techniques for refugee distribution that promote justice, stability, and efficiency.
In the field of refugee allocation, previous studies have combined both optimization algorithms and policy analysis. For instance, the study by Hagen applied a quota adjustment algorithm based on mechanism design for fair, efficient, and strategy-proof allocation [18]. Similarly focused on fairness, Armas et al. employed multi-objective optimization with integer linear programming to balance integration, host priorities, and refugee preferences [19]. Conversely, Janmyr and Stevens analyzed legal and policy frameworks to demonstrate flexible protection in the Middle East, while Nandy’s media analysis revealed how narratives influence migration policy [20], [21]. These approaches deepen understanding of refugee allocation, with positive contributions to fairness and efficiency tempered by practical and societal challenges.
Next, the social integration challenges are highlighted by Almohamed et al., including cultural barriers, language obstacles, and stereotypes [22]. Moreover, Klugman et al. pointed out gender inequalities in refugee policies, particularly restrictions on women’s [23]. As Figure 4 summarizes, the 10 largest refugee-hosting countries imposed more than 75 economic restrictions on women, including limitations on business, banking, and property ownership. Over the past decade, while Colombia and Pakistan made gradual progress, most host nations retained restrictive policies. Thus, the role of refugee-led organizations in Jordan, Lebanon, and Turkey shows how they provided essential aid, social protection, and cultural support despite legal and financial obstacles [24].
Figure 4: Number of legal barriers to women’s employment in the 10 largest refugee-hosting countries [23]
Building on these insights, research on refugee allocation has explored mathematical models to optimize outcomes. Álvarez stated that relocation mechanisms often struggled with inefficiencies in preference matching and fairness [25]. Taking a different route, Bansak & Paulson showed that machine learning could significantly enhance refugee employment outcomes by up to 70% [26]. Besides, Xepapadeas and Mourtos developed sequential and cooperative allocation mechanisms that achieve Pareto efficiency [27], whereas Aziz et al. created a strategy-proof algorithm for stable matching [28]. Expanding on optimization models, Jones and Teytelboym emphasized that matching theory effectively balances refugee and host preferences, similar to school choice mechanisms [29]. Cilali et al. argued that socio-cultural and logistical factors went beyond numerical allocation [30]. Figure 5 illustrates these complexities, highlighting challenges such as camp expansion, resource management, and service provision.
Figure 5: Refugee-related problems [30]
In addition, Ahani et al. introduced a stochastic programming model that outperformed traditional allocation methods in real-world applications [31], while Delacrétaz et al. advocated for preference-based mechanisms to enhance overall efficiency [32]. Together, these studies underscore the importance of stability-driven, optimized strategies for improving refugee resettlement.
Although many previous studies have explored refugee allocation using various algorithms and matching strategies, three significant research gaps remain. Firstly, existing studies have either focused on stability such as HFPDA [28] and Pareto optimization [30], but none have systematically integrated both in the context of refugee allocation at the provincial level. Additionally, some previous studies have applied heuristic algorithms, machine learning, or optimization techniques [26]. Still, none leveraged OMOPSO algorithm in combination with SMT (particularly, Gale-Shapley algorithm) to identify Pareto-optimal allocations in a multi-objective and conflicting space. Finally, most prior studies have considered only a one-time static allocation without accounting for changes in economic, political, or security conditions, like Hagen criticized the EU’s rigid quota system [21].
| Contribution | Algorithm / Matching type | Author and Publication |
| Distributing refugees within the EU | Quota adjustment mechanism | Hagen [18] |
| Improve decision-making in refugee resettlement | Multi-objective integer linear programming (ILP) model | Armas et al. [19] |
| How refugee protection works, looking at international laws, agreements in the area | Analyzes legal frameworks, state policies, institutional roles, and humanitarian practices | Janmyr, Stevens [20] |
| Analyzes specific refugee crisis portrayals, ethical, political media roles | Comparative case study approach to match media sources or themes across regions | Nandy [21] |
| Designing RAS support technology during resettlement | Conceptual Framework | Almohamed et al. [22] |
| Improving international community responds to global refugee crises | Comprehensive Refugee Response Framework (CRRF) | Klugman et al. [23] |
| Describing what RLOs do | Qualitative analysis | El-Abed [24] |
| Syrian refugee allocation by quotas | You Request My House – I Get Your Turn (YRM-HIGHT) and Deferred Acceptance (DA). | Álvarez [25] |
| Monte Carlo load balancing | Monte Carlo simulations, load balancing | Bansak, Paulson [26] |
| Developed sequential and cooperative allocation | Pareto-optimal | Xepapadeas, Mourtos [27] |
| Efficient, fair refugee assignment | Hierarchical Family-Proposing Deferred Acceptance (HFPDA) | Aziz et al. [28] |
| Pareto-optimal matching strategies | Pareto-optimal matching | Jones, Teytelboym [29] |
| Proposal multi-goal solution | Pareto-optimal | Cilali et al. [30] |
| Dynamic matching model | Annie MOORE optimization (Matching and Outcome Optimization for Refugee Empowerment), dynamic matching | Ahani et al. [31] |
| Matching with multidimensional knapsack constraints | Preference-based matching mechanisms | Delacrétaz et al. [32] |
Table 1: Summary of recent related research papers by algorithms
1.3. Key Contributions
A well-planned resettlement strategy must balance equity and practicality to create sustainable solutions. Therefore, identifying adequate housing for refugees is a complex task that requires careful assessment of local resources and economic conditions. To address these pressing issues, this study delves into three fundamental questions:
- What key criteria should be prioritized when allocating refugees to provinces to improve economic integration and prevent inefficient resource use?
- What models does the system use to match refugees to provinces?
- How is the refugee allocation problem addressed to optimize efficiency?
In this study, to effectively allocate refugees to provinces, several essential factors are explored. Through a comprehensive literature review and expert insights, we identify criteria that impact allocation balance, including refugees’ skills and the specific needs of host provinces. Outlining these factors helps establish a balanced refugee distribution, preventing undue pressure on local resources.
Additionally, refugee allocation can be optimized using three interconnected models. The Refugee-Province Compatibility Model (RPCM) focuses on aligning refugee characteristics with provincial attributes. Second, the Matching Pair Quality Model (MPQM) evaluates the strength of each pairing. Lastly, the Optimal Fit Calculation Model (OFCM) refines these pairings by prioritizing long-term integration that benefits both refugees and host provinces.
Therefore, the refugee allocation problem is addressed by combining the strengths of Gale-Shapley’s, SMT and OMOPSO. SMT ensures stable pairings between refugees and host provinces based on mutual preferences. OMOPSO then refines these matchings by optimizing key objectives. This hybrid approach enhances overall efficiency by balancing stability with optimal resource allocation, leading to reduced mismatches and improved integration outcomes.
This research presents an innovative approach to refugee allocation by integrating the OMOPSO algorithm with SMT. Together, these advanced methodologies address critical challenges such as placement optimization, equitable resource allocation, and effective refugee-host region matching. The key contributions of this research are as follows:
- This research proposes a decision-making framework that considers refugee skills, adaptability, and host infrastructure to ensure fair placement and evaluate long-term integration, balancing immediate needs with sustainable resettlement.
- The framework integrates three models to provide a scalable and stable solution for refugee allocation: RPCM evaluates compatibility using Manhattan distance and OMOPSO; MPQM converts discrepancies into satisfaction via an exponential utility function; and OFCM assesses overall fit and ensures stability using the Gale–Shapley algorithm.
- This hybrid model combines OMOPSO’s adaptive search with the stability of the Gale–Shapley method to enhance refugee placement. OMOPSO handles evolving crises, while Gale-Shapley ensures robustness despite incomplete data. This hybrid approach reduces quota waste, improves resource use, and offers a dynamic, data-driven solution for global allocation.
II. Problem Definitions
Our study focused on distributing refugees across different provinces within a single host country to prevent overcrowding, which posed challenges for both the local population and the refugees. This issue can be articulated as Refugee Allocation Optimization Issues (RAOI). In technical terms, the two players involved in RAOI, refugees and provinces, are categorized into limited sets R and P, respectively.
- The set of refugees is defined
R =r0,..,rN, where each ri is the ith refugee in which 0iN, and NN is the total number of refugees. - The set of provinces within a host country is represented as P=p0, .., pM, where each pj is the jth province in which 0jM, and MN is the total number of provinces.
- Each province pj having a maximum capacity cj.
- The allocation is represented by the function: μ:R P{} , assign each refugee ri to at most one province pj such that the number of refugees at pj denoted |μ-1(pj)| does not exceed cj.
A stable matching is achieved when no blocking pair exists. No blocking pair means there is no ri and pj where:
- ri prefers pj over μ(ri) (or if unassigned).
- pj prefers ri over at least one refugee in μ-1(pj) or has capacity remaining |μ-1(pj)| <cj.
If this happens, the allocation becomes unstable, leading to significant consequences.
To illustrate the research issue mentioned above, we use a tabular dataset on the distribution of refugees. The dataset includes three Middle Eastern refugees (Refugee 1 to Refugee 3) who are seeking resettlement in three distinct host provinces (Province 1 to Province 3). Each refugee has their own needs and expectations, similarly, each host province has specific capacities to meet these needs. The criteria for matching refugees with host provinces based on mutual compatibility are demonstrated below:
| Feature | Expected quality of life (HDI) | Ability to obtain employment (%) | Financial support (USD) | Quality of life (HDI) | Labor market capacity (%) |
| 0.75 | 60 | 30 | – | – | |
| 0.65 | 50 | 25 | – | – | |
| 0.80 | 70 | 40 | – | – | |
| – | – | 35 | 0.85 | 65 | |
| – | – | 30 | 0.75 | 55 | |
| – | – | 50 | 0.90 | 75 |
Table 2: Example dataset for RAOI in the Middle East
Accurately defining the traits of both sides is essential to comprehend the connection between refugees and the provinces within the host country. The work of Bansak and Paulson [26] highlights key factors that help identify refugee needs and optimize their integration into host society.
As measured by the Human Development Index (HDI), quality of life (riQL) is the most important factor. Additionally, the social housing ratio (riH), representing the proportion of state or nonprofit-provided apartments for specific groups, refugees’ health status (riHN), valued at 1 if medical issues are present and 0 otherwise. The ability to find employment (riJE), measured by the success rate of securing a job within two years of resettlement, and expected financial support (riJS), quantified in USD.
For provinces, there should also be characteristics and constraints put in place to ensure the appropriateness of refugee reception, optimizing the use of available resources. In particular, high quality of life (pjQL), as reflected by the HDI, is often associated with better reception than places with less favorable living conditions.. Moreover, well-developed social housing ratio (pjH) and health systems (pjHN) make it easier for refugees to access essential services and settle in effectively. In addition, the labor market capacity of the province is also a determining factor. Sectors with vibrant labor markets (pjLM), especially in occupations in which refugees have expertise, will facilitate their participation in the economy. Lastly, financial support (pjFS) provides refugees with essential resources to help them overcome the initial challenges of the settlement process.
| Players | Refugees ri | Provinces pj |
| Key Characteristics | Quality of Life (riQL) | Quality of Life (pjQL) |
| Employment Ability (riJE) | Labor Market Capacity (pjLM) | |
| Social housing ratio (riH) | Social housing ratio (pjH) | |
| Expected financial support (riFS) | Financial support (pjFS) | |
| Health status (riHN) | Health System (pjHN) |
Table 3: The characteristics of refugees and provinces
The refugee allocation problem involves balancing multiple objectives: as highlighted by Bansak and Paulson [26], refugees tend to favor provinces offering a high quality of life(riQL) and job prospects (riJE), while provinces assess refugees based on labor capacity (pjLM) and financial needs (pjFS). These goals often conflict – provinces with jobs may lack financial resources, and desirable locations may face resource strain. The system uses OMOPSO for preference ranking and Gale-Shapley for stable matching, navigating trade-offs between integration, welfare, and sustainability. For example, a refugee needing aid (riFS) might be matched with a financially supportive province (pjFS) but with fewer job options, highlighting the tension between short-term needs and long-term outcomes. This iterative process is illustrated in the flowchart below, aiming to optimize social integration, economic stability, and resource efficiency while addressing the inherent tensions in multi-objective decision-making.
Figure 6: The process modeling of the RAOI problem
The flowchart presents a method for allocating refugees in the Middle East. The process starts with collecting data on refugees, host provinces, and constraints. Next, the collected data is analyzed to extract key characteristics. To optimize allocation strategies, crossover combines existing allocation plans to generate diverse offspring solutions, while mutation introduces random adjustments to maintain solution diversity. After identifying feasible solutions, OMOPSO creates preference lists using multi-objective criteria. These are then input into the Gale-Shapley algorithm to form stable matches, followed by a fitness function to assess match quality for optimal refugee allocation.
III. Methods
3.1 Existing model
To address the RAOI, our research refers to ILP (Integer Linear Programming) – an established mathematical model originally designed for the Maximum size Stable Matching problem with Ties and Incomplete lists (MAX-SMTI) [33]. This model shares significant similarities with RAOI as they all involve constrained and prioritized matching problems under incomplete and possibly tied preference lists. In order to better illustrate the ILP model, the following table provides a detailed view of how each model component can be adapted:
| Component | Description |
| Agents | M: Set of agents on one side.W: Set of agents on the other side.AMW: Set of acceptable pairs based on the preference lists. |
| Decision Variables | xi,j=1 if iM is matched to jW ,xi,j=0 otherwise. |
| Objective Function | Function used to maximize the number of matched pairs:max (i,j)A xi,j |
| Constraint 1 | Each agent is matched to at most one agent:iA(j)xi,j1 , jA(i)xi,j1 |
| Constraint 2 | Stability constraint:xi,j+i’ jixi’,j+j’ ijxi,j’1 for all unmatched (i,j)A |
| Constraint 3 | Binary variables:xi,j{0,1} for all (i,j)A |
Table 4: The ILP formulation for the MAX-SMTI solving
3.2 Model for RAOI
Based on the characteristics and the requirements in the Problem Definitions section, the following mathematical model named RAOI will be introduced as follows:
RAOI={(R, P), (ri,pj),Q(ri , pj), f)}
Where:
R =r0,..,rN: A finite set of refugees, where each ri is the ith refugee,0iN, and NN, and N is the total number of refugees.- P=p0, .., pM: A finite set of provinces in the host provinces, where each pj, is the jth province 0jM, and MN, and M is the total number of provinces. Each province pjhas a limited capacity (maximum number of refugees it can host).
- ri =riQL, riJE, riH, riFS, riHN: Set of refugees, each with specific characteristics and preferences.
- pj=pjQL, pjLM, pjH, pjFS, pjHN: Set of provinces, each with distinct capacities and attributes.
- Q(ri , pj): Function to evaluate a province pj based on a refugee’s characteristics ri
- f: Fitness function to evaluate the fitness value after matching iterations are terminated.
This formulation outlines the basis of refugee-province allocation, with RAOI operationalized through three interconnected models RPCM, MPQM, and OFCM used sequentially for compatibility, satisfaction assessment, and overall optimization, as follows:
- RPCM assesses compatibility between refugee and city attributes using Manhattan distance, also known as the ‘city block distance’, forming the basis for evaluating mutual satisfaction [34]. The allocation is then optimized using OMOPSO, which effectively handles multiple objectives in the pairing process.
- MPQM assesses pairing quality by analyzing the needs of refugees and provinces, using an exponential utility function based on Manhattan distance for compatibility.
- OFCM ensures stable and balanced pairings by applying the Gale–Shapley algorithm, where refugees propose and provinces respond. It evaluates overall fitness to support long-term integration and system stability.
To ensure consistent comparisons between the attributes of refugees and the host province for each pair, the model first normalizes the data. Specifically, it normalizes the ability to find work and social housing ratio as follows kx100 where kx is the value of the attribute x . For financial support, the Sigmoid is applied as shown below:
xsigmoid = 11+e-(kx-) (1)
Where μ represents the mean of the dataset, and σ represents the standard deviation of the dataset.
Then, the model measured the degree of difference between the characteristics of refugees and host provinces by Manhattan formula:
dManhattan(A,B)=x = attributewx.|ax – bx| (2)
Where A,B are the points needed to calculate the Manhattan distance and ax, bx is the attribute value of points A or B. After applying the data standardization steps with (1), (2), the degree of difference d(ri , pj) for both sides is divided as follows:
dno-norm(ri, pj)=wQL.|riQL – pjQL|+wHN.|riHN – pjHN| (3) dlinear (ri, pj)=wH.|riH100 -pjH100|+wJE.|riJE100 – pjJE100| (4)
dsigmoid (ri, pj)=wFS.|11+e-(riFS-) -11+e-(pjFS-)| (5)
Finally, the total degree of difference between refugee and province is calculated as the sum of the three components:
d(ri , pj) =dno-norm(ri, pj) +dlinear (ri, pj) +dsigmoid (ri, pj) (6)
Where: wx is the weight representing the priority of the refugee or the receiving province in the matching process. These weights satisfy: x =1wx = 10 and wx 0, x
The weights can be adjusted based on the priorities of the refugees wi or the host province wi, corresponding to dr(ri , pj) and dp(ri , pj), respectively.
Following the computation of differences, the MPQM model evaluates the overall quality of each refugee–province pair. The pairing quality Q(ri , pj)takes into account both sides’ satisfaction and is defined as:
Q(ri , pj)= .Sr(ri , pj) + .Sp(ri , pj) (7)
Where:
Sr(ri , pj): The level of satisfaction ri when matched pj is calculated as:
Sr(ri , pj)=1- dr(ri , pj)max dr(ri , pj) + e (8)
Sp(ri , pj): The level of satisfaction pj when matched ri is computed as:
Sp(ri , pj)=1-dp(ri , pj)max dp(ri , pj) + e (9)
, : The weight reflects the priority level of each party, with +=1
Accordingly, the satisfaction of each party is calculated using the difference level measured in RPCM. These values reflect the quality of the match, with higher values indicating closer matches and lower values indicating less suitable pairings.
Finally, the f() metric in the OFCM model computes the mean satisfaction scores to assess the effectiveness of the allocation strategy. This function combines the satisfaction scores derived from the MPQM model.
f()=1ni =1nQ(ri , pj) (10)
where n is the total number of refugees. This formula determines the optimal refugee allocation by maximizing overall satisfaction.
The flowchart below outlines the process of allocating refugees (R) to provinces (P) using three interconnected models: RPCM, MPQM, and OFCM. It begins with input data (R and P), which is processed through RPCM to normalize characteristics, calculate the difference d(ri , pj) using Manhattan distance, and optimize these differences with OMOPSO. The optimized d(ri , pj) is then fed into MPQM, which calculates the pair quality Q(ri, pj) based on satisfaction levels of both refugees and provinces. Finally, OFCM uses Q(ri, pj) to perform stable matching via Gale-Shapley and evaluate the overall fitness, producing an optimal allocation of refugees to provinces.
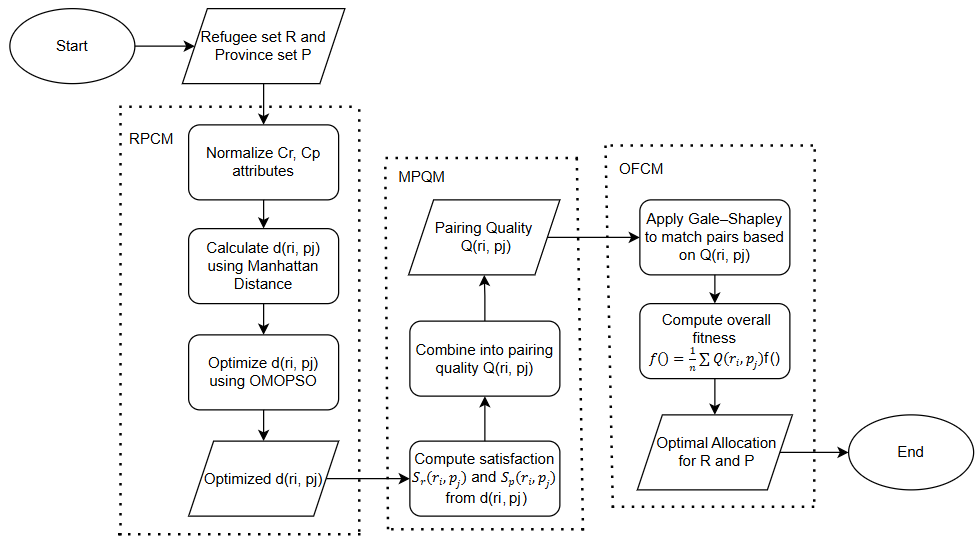
Figure 7: The process flow of RAOI model interconnection
The RPCM, MPQM, and OFCM models offer a structured, quantifiable approach to refugee-province matching by measuring compatibility and satisfaction. RPCM normalizes diverse attributes and applies Manhattan distance for fair comparison. MPQM incorporates both sides’ satisfaction for balanced pairing, while OFCM aggregates these scores to evaluate overall allocation quality. Computationally, these models are efficient and scalable due to normalization and distance-based calculations. However, their reliance on static weights and fixed inputs limits adaptability in dynamic contexts. To address this, the next section introduces OMOPSO—a dynamic, multi-objective approach that refines preferences and enhances matching stability under changing priorities and constraints.
3.3 Algorithm
NP-hard problems are inherently difficult to solve efficiently, not solvable in polynomial time, and thus must be approached through approximation or heuristic methods [35]. The RAOI problem falls into this category due to two key challenges: the exponential growth of possible refugee-province pairings ri,pj as the size of R and P increases, making exhaustive evaluation impractical, and the instability caused by the presence of blocking pairs. Therefore, this study joined SMT and the OMOPSO algorithm to effectively tackle the complexity of the RAOI problem. OMOPSO employed Pareto principles to balance trade-offs, then the Gale-Shapley algorithm from SMT ensured a stable matching by systematically eliminating blocking pairs, assuming the input preferences were complete and consistent.
To be more precise, the primary purpose of the Gale-Shapley algorithm in our study is to operate within the OFCM model, immediately after the results from the MPQM model are collected, in order to prevent blocking pairs. It operates interactively where ri propose to pj in order of preference, and pj accept or reject based on their preference lists and capacity. Particularly, the algorithm’s effectiveness depends on the construction of priority lists for both parties, which are quantitatively modeled based on the attributes presented in Table 8. From the refugee’s perspective, the priority score for province pj is determined by the function sri,pj=w1pjQL+w2pjFS+w3pjHN+w4riH-pjH, which reflects factors like quality of life, financial support, health system and housing compatibility. Conversely, each province evaluates refugee candidates based on the scoring function spj,ri=w5riEA+w6riHN-w7max0, riFS-pjFS, which indicates quality of life, financial support and health. This process repeats until no blocking pairs remain, ensuring that the final pairings are stable and optimal for both parties.
The study integrates the OMOPSO algorithm with the Gale-Shapley algorithm to tackle the RAOI problem, which seeks to optimize the allocation of refugees (R) to provinces (P) based on quality and stability. OMOPSO conducts multi-objective optimization, exploring a vast solution space to identify optimal refugee-province matches (ri, pj) while adhering to capacity constraints. However, to guarantee the elimination of blocking pairs, where ri and pj mutually prefer each other over their current matches, the Gale-Shapley algorithm is subsequently employed. This algorithm utilizes preference lists derived from Q(ri, pj), enabling refugees to propose to provinces in order of preference, while provinces accept or reject proposals based on their own evaluations, thereby ensuring stable outcomes.
In the dimensions of the RAOI, chromosomes are candidate solutions that represent encodings for allocating refugees to provinces. Each chromosome is represented as [a, b, c], where:
- a, b, c are the numbers of people to be allocated to 3 different provinces
- Satisfy the constraint: a + b + c = 10 (total number of people to be allocated)
In Figure 10, chromosome [1, 6, 3] represents the solution to allocate 1 person to location 1, 6 people to location 2, 3 people to location 3.
Figure 8: Visual representation of a chromosome
The algorithm begins by randomly generating an initial population of chromosomes that satisfy the total allocation constraint. During each iteration, chromosomes are evaluated using a fitness function (see Equation 9), and the best-performing individuals are selected as pBest/gBest to guide the velocity update. Then, the mutation operator is performed to create diversity, with an automatic adjustment mechanism to ensure that the total number of people is always 10. The best chromosomes are stored in the Pareto archive if they are non-dominated, meaning none of them is strictly better than another in all objectives.
Figure 9: The process of chromosome
In order to facilitate comprehension, our research proposes a flowchart illustrating the step-by-step application of OMOPSO and Gale-Shapley algorithm to solve the refugee allocation problem.
Figure 10: The flowchart of OMOPSO and Gale-Shapley integration for RAOI.
The process begins with collecting input information from the characteristics of refugees R={r1,…,rN} and provinces P={p1,…,pM} and then initializing the population of chromosomes, where each chromosome is a vector representing the number of refugees allocated to each province. Next, the OMOPSO algorithm evaluates the suitability of each chromosome. It stores the non-dominated solutions in the repository and updates velocity and position parameters through iterations to enhance solution quality. Once no further improvement is observed, the system passes the best solutions to the Gale-Shapley algorithm. The Gale-Shapley algorithm, using preference lists constructed based on the attributes of refugees and provinces, generates a stable matched set by eliminating blocking pairs. Finally, the system then verifies the stability of the allocation, looping back to initialization if unstable, before displaying the final output.
To effectively address the refugee-province allocation problem, a hybrid algorithm combining OMOPSO and Gale-Shapley is used. The OMOPSO algorithm begins by initializing a swarm of particles representing potential refugee-province matchings (line 1). Each particle’s fitness is evaluated using function F(S(ri, pj)) (line 1), and both personal and global bests are updated accordingly (lines 12–15). The positions and velocities of particles are then adjusted (lines 17–18) to explore better solutions.
Figure 11: Pseudocode for optimal matching using OMOPSO and Gale-Shapley
The Gale-Shapley algorithm complements this by ensuring stability in matchings (line 06). Refugees propose to provinces following preference order (lines 07–09), and provinces accept or reject based on their own preferences. This two-phase optimization ensures both quality and stability in the final assignments.
IV. Result
The experiment evaluated the effectiveness of the GS algorithm combined with OMOPSO in balancing solution diversity and optimization performance. The server configuration utilized for this problem possesses the following technical specifications: Microsoft’s Windows 11 as operating system, powered by an 11th Gen Intel® Core™ i5-1135G7 processor (2.40GHz, 4 physical cores, 8 logical threads) and equipped with total memory 7.7 GiB. The parameters of the algorithms are presented below:
| Algorithm Parameter | Population size | Number of generations | Max time (s) | Crossover rate | Mutation rate | Distributed cores |
| Value | 100 | 500 | 60 | 0.9 | 0.1 | All cores |
Table 5: The table of input algorithm parameters.
Subsequently, we introduce a tabular dataset detailing 10 characteristics of 4,400 refugees and 44 provinces, with edge weights in the range [1;10]. This dataset is partially inspired by and calibrated using publicly available statistics from the IIED report on Syrian refugees in Jordan, which includes demographic and socio-economic indicators relevant to refugee-host integration [1]. Although the complete micro-level data were not accessible, we reconstructed key variables such as quality of life, related financial/employment factors based on aggregated values and reported distributions. Each entity lists requirements (req) with corresponding weights (w), reflecting the importance of each preference or constraint. A higher weight indicates that the corresponding requirement is more critical in the entity’s evaluation process. Additionally, properties (pro) represent quantifiable attributes or features that are essential in the matching process.
by “req-w-pro 0 to 10.req-w-propreferences
| r1 | r2 | r3 | p1 | p2 | p3 | |
| Quality of Life | 0.36-5-0 | 0.34-3-0 | 0.79-6-0 | 0-0-0.89 | 0-0-0.9 | 0-0-0.59 |
| Ability to obtain employment | 0.86-5-0 | 0.76-10-0 | 0.37-1-0 | 0-0-0.62 | 0-0-0.35 | 0-0-0.93 |
| Social housing ratio | 0.24-3-0 | 0.41-7-0 | 0.11-6-0 | 0-0-0.5 | 0-0-0.16 | 0-0-0.01 |
| Expected financial support | 0.88-9-0 | 0.05-9-0 | 0.5-6-0 | 0-0-0.89 | 0-0-0.03 | 0-0-0.64 |
| Health status | 0.19-2-0 | 0.96-7-0 | 0.67-2-0 | 0-0-0.21 | 0-0-0.72 | 0-0-0.56 |
| Quality of Life | 0-0-0.57 | 0-0-0.6 | 0-0-0.51 | 0.73-6-0 | 0.94-1-0 | 0.96-9-0 |
| Labor Market Capacity | 0-0-0.14 | 0-0-0.4 | 0-0-0.23 | 0.21-7-0 | 0.42-4-0 | 0.69-1-0 |
| Social housing ratio | 0-0-0.7 | 0-0-0.64 | 0-0-0.56 | 0.3-4-0 | 0.81-8-0 | 0.47-7-0 |
| Financial support | 0-0-0.19 | 0-0-0.96 | 0-0-0.77 | 0.05-6-0 | 0.85-3-0 | 0.18-3-0 |
| Health status | 0-0-0.93 | 0-0-0.38 | 0-0-0.82 | 0.94-1-0 | 0.06-2-0 | 0.31-1-0 |
Table 6: Sample dataset of refugees and provinces
With the above dataset, this section presents a clearer overview of the empirical results by summarizing the main aspects through a system of tables and illustrative diagrams. We applied 8 algorithms (OMOPSO, NSGA-II, NSGA-III, eMOEA, PESA2, VEGA, IBEA, SMPSO) to help determine which algorithm performs best on the dataset of 4400 individuals.
| No. | eMOEA | VEGA | NSGAII | NSGAIII | SMPSO | IBEA | PESA2 | OMOPSO |
| 1 | 245235 | 271620 | 357198 | 373715 | 33609 | 315827 | 288762 | 399225 |
| 2 | 252751 | 269890 | 355104 | 376087 | 336088 | 315570 | 297251 | 403444 |
| 3 | 248562 | 271192 | 360293 | 376620 | 331276 | 318205 | 295950 | 395753 |
| 4 | 254719 | 268316 | 353173 | 377986 | 336835 | 316393 | 288967 | 397877 |
| 5 | 248606 | 275957 | 352573 | 377645 | 337485 | 311529 | 290418 | 395542 |
| 6 | 254287 | 267906 | 353754 | 376669 | 339403 | 312713 | 289194 | 396844 |
| 7 | 254552 | 269097 | 353448 | 383403 | 338620 | 317246 | 287872 | 396046 |
| 8 | 248047 | 267578 | 356551 | 374219 | 330869 | 314556 | 297352 | 404504 |
| 9 | 252586 | 268107 | 352385 | 374943 | 334753 | 317098 | 295112 | 396214 |
| 10 | 252470 | 271452 | 361679 | 383558 | 335505 | 314681 | 293705 | 397944 |
Table 7: Fitness evaluation of eight genetic algorithms
These algorithms belong to different groups, such as multi-objective optimization based on search methods (OMOPSO and NSGA-III), simple evolutionary algorithms VEGA, partitioning algorithms PESA2, and index-based algorithms IBEA. This difference facilitates comparison from multiple perspectives, particularly in terms of fitness and running time, which helped determine the optimal algorithm in this case (OMOPSO or NSGAIII). However, the choice of OMOPSO [36] for solving the allocation problem is supported by the results in Table 7, where it consistently achieved the highest fitness values across most test cases, demonstrating its superior solution quality in practice.
- Iteration 1 b) Iteration 2
c) Iteration 3 d) Iteration 4
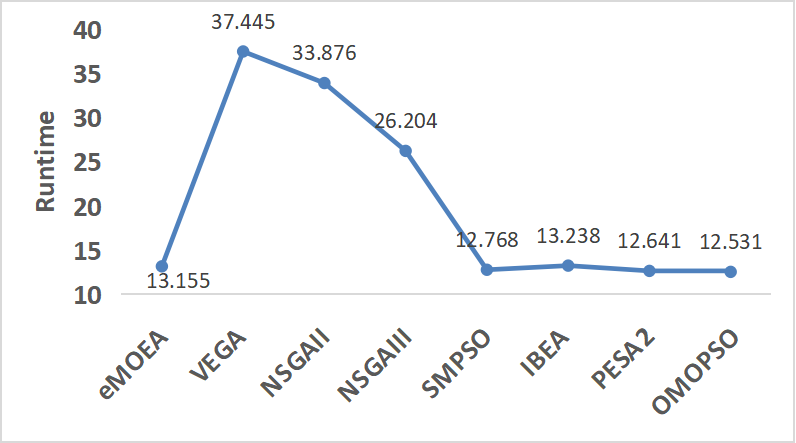
Figure 12: Comparison of 4400 individuals’ runtimes (in seconds) for the 8 algorithms
The figure presents the runtime comparison of eight algorithms across four distinct iterations. As illustrated, OMOPSO consistently maintains low and stable execution times relative to other methods, with negligible fluctuations between runs. In iterations 1 to 3, while algorithms such as VEGA and NSGAII show significant spikes in runtime, OMOPSO remains under 15 across all cases. In iteration 4, where overall runtimes drop, OMOPSO continues to perform efficiently and consistently. PESA2 [37], with a moderate fitness, demonstrated a good exploration/exploitation balance, while eMOEA [38] and IBEA [39] offered faster runtimes but lower fitness values, making them appropriate for speed-sensitive scenarios. In contrast, VEGA [40] and NSGA-III [41] showed weaker performance, reinforcing OMOPSO’s advantage across accuracy and efficiency. OMOPSO also outperformed NSGA-II [42] and SMPSO [43] in fitness and runtime balance, demonstrating its robustness against diverse algorithmic strategies. These results demonstrate that OMOPSO offers both computational efficiency and stability, making it the most suitable choice for the refugee allocation problem. To further illustrate the outcomes, figure 13 below depicts refugee satisfaction levels across different provinces.
Figure 13: Matching results between refugees and provinces
OPSO, NSGA-II, across 44 provinces,selection of these 44 nd SMP. selec
Figure 13 illustrates that OMOPSO maintains stable satisfaction levels across provinces and iterations, demonstrating both solution quality and algorithmic robustness. OMOPSO achieves the highest fitness (403,444) with a competitive runtime (13.61 s), confirming its suitability for large-scale and accuracy-sensitive problems such as refugee resettlement. SMPSO (392,723) and NSGA-III (392,263) also perform well in terms of fitness but show greater variability in runtime. NSGA-II attains a fitness of 370,540; however, its prolonged and unstable runtimes limit its practical applicability. In contrast, PESA2 and IBEA yield moderate performance, while eMOEA and VEGA are faster but produce significantly lower fitness outcomes. Overall, OMOPSO presents the best balance of accuracy, runtime efficiency, and consistency, making it the most suitable algorithm for refugee allocation optimization.
V. Discussion
The experimental results demonstrate OMOPSO’s superior performance, achieving the highest average fitness score (404504) and the fastest average runtime (14.10s), significantly outperforming baseline algorithms like eMOEA and VEGA (Table 7). Compared to NSGA-II and NSGA-III, OMOPSO balances solution quality and efficiency better, due to its swarm-based design. These findings align with Kachitvichyanukul et al., who highlighted PSO’s advantages in convergence and diversity over traditional genetic approaches [13]. Unlike prior studies that separated fairness and stability in refugee matching, our experiment integrates both: OMOPSO optimizes conflicting multi-objective criteria, while Gale-Shapley ensures stable pairings. This hybrid framework comprising RPCM, MPQM, and OFCM extends Andersson et al. by adding Pareto efficiency [27] and advances Aziz et al. by embedding evolutionary optimization into a scalable, unified system [28]. However, this study is limited by the use of static input data and fixed priority weights, which may not reflect dynamic refugee or regional changes. Future research should focus on real-time adaptive models that incorporate live data streams and machine-learned weight adjustments to enhance decision-making responsiveness and realism.
VI. Conclusion
The uneven distribution of refugees among provinces in the Middle East has caused economic imbalances, social instability, and resource overload in certain regions, making the resettlement of refugees an urgent issue. To address this problem, our study proposed a two-phase approach combining OMOPSO and SMT. OMOPSO was applied to navigate complex multi-objective constraints, identifying feasible allocation scenarios, while SMT, specifically the Gale-Shapley algorithm, was used to ensure stable pairings based on individual preferences. Besides, a major contribution of this research is the design of a hybrid model that optimizes refugee allocation fairly and stably. It enhances matching efficiency while aligning refugee needs with provincial capacities. Accordingly, our approach was validated through a simulated refugee allocation scenario, confirming the effectiveness of combining OMOPSO and Gale-Shapley in achieving high satisfaction. Compared to eight other algorithms, OMOPSO showed the best balance of fitness and runtime, highlighting its efficiency and robustness for solving RAOI. Ultimately, this research contributes to the field of fairer refugee distribution strategies and facilitates policymakers and humanitarian organizations to gain valuable insights, supporting sustainable regional development.
References
[1] A. H. Salam, P. Garcia Amado, and A.-B. Yamen, “Syrian refugees in Jordan”, Sep. 2024. Available: https://www.iied.org/22486iied
[2] G. T. Maria and A. Dana, “Understanding Syrian migration in Lebanon: a methodological framework”. European Commission, Sep. 06, 2023. DOI:10.12688/openreseurope.16261.1
[3] F. Muath, “Mafraq educators pin hopes on donors to ease pressure off refugee-burdened school system”. The Jordan Times, Mar. 30, 2016 Available: https://www.jordantimes.com/news/local/mafraq-educators-pin-hopes-donors-ease-pressure-refugee-burdened-school-system
[4] E. Balla, “The European Union’s Response to the Syrian Refugee Crisis”. E-International Relations, 2023. Available: https://www.e-ir.info/pdf/101195
[5] D. Brown, M. Morris, and L. Thompson, “Urban protracted displacement and displacement economies”. Environment and Urbanization, vol. 36, no. 1, pp. 123–140, Apr. 2024, DOI: 10.1177/09562478241277087
[6] G. Honein-AbouHaidar, L. Bou-Karroum, S. E. Parkinson, et al., “Integrating Syrian refugees into Lebanon’s healthcare system 2011–2022: a mixed-method study”. Confl. Health, vol. 18, Suppl. 1, p. 43, 2024. DOI: 10.1186/s13031-024-00600-w
[7] I. Y. Addo and A. Tanle, “Rethinking solutions for protracted refugee situation: A case study of the Buduburam refugee camp closure in Ghana”. Scientific African, Jun. 7, 2023. DOI: 10.1016/j.sciaf.2023.e01746
[8] P. Biró, “The stable matching problem and its generalizations: an algorithmic and game theoretical approach”. Available: https://www.cs.bme.hu/~pbiro/biro_dissertation.pdf
[9] T. Ekim, “The Nobel Prize in Economic Sciences 2012 and Matching Theory”. Science And Technology Publications, 2020. DOI: 10.5220/0009459600050016
[10] D. Gale and L. S. Shapley, “College Admissions and the Stability of Marriage”. Math. Assoc. Am., Jan. 1962. DOI: 10.1080/00029890.1962.11989827
[11] A. Teytelboym, D. Delacretaz, and S. D. Kominers, “Matching Mechanisms for Refugee Resettlement”, Sep. 21, 2020. DOI: 10.1257/aer.20210096
[12] J. Zhang, J. Cao, F. Zhao et al., “A constrained multi-objective optimization algorithm with two cooperative populations”. Memet. Comput., vol. 14, pp. 95–113, 2022. DOI: 10.1007/s12293-022-00360-1
[13] M. Arjmand, A. A. Najafi, and M. Ebrahimzadeh, “Evolutionary algorithms for multi-objective stochastic resource availability cost problem”. OPSEARCH, vol. 57, pp. 935–985, 2020. DOI: 10.1007/s12597-020-00447-8
[14] D.-X. Liu, Y.-R. Gu, C. Qian, X. Mu, and K. Tang, “Migrant resettlement by evolutionary multiobjective optimization”. IEEE Trans. Artif. Intell., vol. 6, no. 1, pp. 51–65, 2024. DOI: 10.1109/TAI.2024.3443790
[15] A. Rajani, D. Kumar, and V. Kumar, “Impact of controlling parameters on the performance of MOPSO algorithm”. Procedia Comput. Sci., vol. 167, pp. 2132–2139, 2020. DOI: 10.1016/j.procs.2020.03.261
[16] Y. Liu, Y. Li, and D. Huang, “A multiobjective optimization model for continuous allocation of emergency rescue materials”. Math. Probl. Eng., vol. 2020, Article ID 5693182, 2020. DOI: 10.1155/2020/5693182
[17] A. Garces-Jimenez, J. M. Gómez, N. Gallego-Salvador, and A. J. García-Tejedor, “Genetic and swarm algorithms for optimizing the control of building HVAC systems using real data: A comparative study”. Mathematics, vol. 9, no. 18, Art. no. 2181, 2021. DOI: 10.3390/math9182181
[18] M. Hagen, “Refugee relocation: A mechanism design approach”. The Economic Journal, Volume 134, Issue 663, October 2024, Pages 3027–3046. DOI: 10.1093/ej/ueae028
[19] J. D. Armas, V. Bélanger, G. Laporte, and M. Rancourt, “Optimizing the assignment decisions in the refugee resettlement process”. International Transactions in Operational Research, Mar. 2025. DOI:10.1111/itor.70017
[20] M. Janmyr and D. Stevens, “Regional Refugee Regimes: Middle East”, 2020. DOI:10.13140/RG.2.2.31446.06723.
[21] D. Nandy, “The Representation of Refugees in the Media of the Middle East and Europe: A Comparative Study. In Nasir Uddin and Delaware Arif (eds.)”. Refugees and the Media: Local and Global Perspectives, Palgrave Macmillan, Gewerbestrasse, pp.115-136, 2024. DOI:10.1007/978-3-031-46514-7_7.
[22] A. Almohamed, D. Vyas, and R. Talhouk, “Towards a Conceptual Framework for Understanding the Challenges in Refugee Re-settlement”. Proc. ACM Hum.-Comput. Interact., vol. 6, pp. 1-27, 2022. DOI: 10.1145/3492856
[23] J. Klugman, E. Ortiz, and A. H. Rubin, “Key Challenges for Refugee Policies and Programs: A Gender Perspective”. World Bank, 2022. Available: https://documents1.worldbank.org/curated/en/447911643215960323/pdf/Key-Challenges-for-Refugee-Policies-and-Programs-A-Gender-Perspective.pdf
[24] O. El-Abed, M. Hoshmand, F. al Hamouri, and W. Najdi, “Refugee communities mobilising in the Middle East: Refugee-led organisations in Jordan, Lebanon, and Turkey.”, Apr. 2023. Available: https://lebanesestudies.com/wp-content/uploads/2023/07/LERRN_RLO_Study_Middle_East_Final_Report_may_16.pdf
[25] L. Álvarez, “Two effective solutions from matching theory”. Lund University, Jun. 2018. Available:https://lup.lub.lu.se/luur/download?func=downloadFile&recordOId=8949111&fileOId=8949121
[26] K. Bansak and E. Paulson, “Outcome-driven dynamic refugee assignment with allocation balancing”. arXiv:2007.03069v5 [math.OC], May. 2024. DOI:10.1287/opre.2022.0445
[27] P. Xepapadeas and I. Mourtos, “Refugee allocation mechanisms: theory and applications for the European Union”. Social Science Research Network (SSRN), Feb. 2021, DOI: 10.2139/ssrn.3812993
[28] H. Aziz, J. Chen, S. Gaspers, and Z. Sun, “Stability and Pareto optimality in refugee allocation matchings”. Proceedings of AAMAS 2018, Stockholm, Sweden, 10–15, Jul. 2018. Pages 964 – 972. DOI: 10.5555/3237383.3237842
[29] A. Teytelboym and W. Jones, “Matching systems for refugees”. Journal on Migration and Human Security, 2017. Available: https://pure.royalholloway.ac.uk/ws/files/28543847/103_353_1_PB.pdf
[30] B. Cilali, K. Barker, and D. G. Andrés, “A location optimization approach to refugee resettlement decision-making”. Sustainable Cities and Society, 2021. DOI: 10.1016/j.scs.2021.103153
[31] N. Ahani, P. Gölz, A. D. Procaccia, A. Teytelboym, and A. C. Trapp, “Dynamic placement in refugee resettlement”. Operations Research, vol. 72, no. 3, pp. 1087–1104, Jul. 18, 2021. DOI: 10.1287/opre.2021.0534
[32] D. Delacrétaz, S. Duke Kominers, and A. Teytelboym, “Matching mechanisms for refugee resettlement”. American Economic Review 113 (10): 2689–2717, 2023. DOI: 10.1257/aer.20210096
[33] M. Delorme, S. García, J. Gondzio, J. Kalcsics, D. Manlove, and W. Pettersson, “Mathematical models for stable matching problems with ties and incomplete lists”. European Journal of Operational Research, vol. 277, no. 2, pp. 426–441, Sep. 2019. DOI: 10.1016/j.ejor.2019.03.017
[34] Z. Yu, K. Wang, S. Xie, Y. Zhong, and Z. Lv, “Prototypical network based on Manhattan distance”. Computer Modeling in Engineering & Sciences, vol. 131, no. 2, pp. 1–21, Mar. 2022. DOI: 10.32604/cmes.2022.019612
[35] S. K. Saini, “A study and explore the significance of NP Hard and Soft Problem”. Journal of Emerging Technologies and Innovative Research, vol.10, Issue 3, Mar. 2023. ISSN-2349-5162
[36] J. Zhang, L. Wang, and Y. Chen, “A comprehensive review of particle swarm optimization”. J. Zhejiang Univ. Sci. C, May. 2024, DOI:10.4028/www.scientific.net/JERA.23.141
[37] H. Jain and K. Deb, “An evolutionary many-objective optimization algorithm using a reference-direction-based non-dominated sorting approach, Part II: Handling preferences and extensions”. IEEE Trans. Evol. Comput., vol. 22, no. 6, pp. 960–984, Dec. 2018. DOI:10.1109/TEVC.2013.2281535
[38] X. Wang, F. Zhang, and M. Yao, “A many-objective evolutionary algorithm with metric-based reference vector adjustment”. Complex Intell. Syst., vol. 10, pp. 207–231, 2024, DOI: 10.1007/s40747-023-01161-w
[39] K. Pereverdieva, A. Deutz, T. Ezendam, T. Bäck, H. Hofmeyer, and M. T. M. Emmerich, “A comparative analysis of indicators for multiobjective diversity optimization”. arXiv preprint, Oct. 2024. DOI: 10.48550/arXiv.2410.18900
[40] T. Andersson, L. Ehlers, and A. Martinello, “Dynamic refugee matching”. Lund Univ. Working Paper, Mar. 2018. Available: https://www.econstor.eu/bitstream/10419/260236/1/wp2018-007.pdf
[41] H. Wang, L. Chen, and Y. Zhang, “An improved NSGA-III algorithm with adaptive reference point adjustment for many-objective optimization”. Appl. Soft Comput., vol. 138, p. 110567, 2023, DOI: 10.1016/j.asoc.2023.110567
[42] P. Kumar, S. Roy, and N. Gupta, “A modified NSGA-II algorithm with adaptive mutation strategy for many-objective optimization”. Appl. Soft Comput., vol. 115, p. 108204, 2023, DOI: 10.1016/j.asoc.2021.108204
[43] T. Ling, Z. H. Zhan, Y. X. Wang, Z. J. Wang, W. J. Yu, and J. Zhang, “Competitive swarm optimizer with dynamic grouping for large scale optimization”. Proc. IEEE Congr. Evol. Comput. (CEC), 2018, pp. 1–8, DOI: 10.1109/CEC.2018.8477971

