Abstract

Internships have become a crucial part of the modern labor market, yet the recruitment process is hindered by mismatches and inefficiencies in identifying suitable interns. These issues are believed to be an obstacle for interns’ career growth, while employers miss the opportunity to harness potential interns. To address these problems, our paper employs Stable matching theory to ensure mutually optimal matches by aligning employer and intern preferences, eliminating unstable pairings where either party prefers another match. This research improves internship recruitment by minimizing mismatches, leading to more effective hiring and better workforce integration. By integrating NSGA-III for multi-objective optimization, this research ensures stable and efficient employer-intern pairings, significantly enhancing recruitment processes and match quality. This approach combines the Gale-Shapley algorithm to ensure stable matches while leveraging NSGA-III to diversify input configurations, overcoming limitations of Gale-Shapley and optimized multi-objective pairings between interns and employers.

Keywords: Intern-Employer Matching, Matching Optimization, Stable matching theory, NSGA-III and Gale-Shapley algorithm.

Introduction

1.1 Background.

In recruitment processes, a common challenge is the mismatch between interns’ expectations and employers’ requirements. Poor leadership and working conditions reduce satisfaction and increase turnover [1]. Mahesh notes that the lack of soft skills of the internship candidates, such as communication, reduces the employability [2]. Figure 1 shows matched jobs yield higher graduate wages.

Figure 1: Pen’s Parade (Quantile Function) for Wage Income per Graduate [3]

A low wage might reduce excitement and severely affect performance [4]. Lack of work discipline and limited experience pose significant challenges to task completion, often leading to missed deadlines and decreased efficiency among interns [5]. For companies and organizations, assigning interns to unsuitable roles not only hampers work efficiency but also disrupts overall productivity. This mismatch results in considerable financial losses and resource drain due to the costs of onboarding and training interns who may not be a good fit, ultimately leading to wasted time, effort, and money [6].

Several strategic conflicts arise during the matching process that must be carefully navigated. Employers prioritize responsibility, adaptability, and growth potential [7], while interns seek flexible hours, training, and advancement [8]. These mismatches hinder recruitment and reduce intern satisfaction. Figure 2 highlights talent shortage disparities, including skill and expectation mismatches.

Figure 2: Discrepancy Between Employers’ and Students’ Expectations on Key Hiring Criteria [9].

Balancing these interests are essential not only for providing interns with practical learning experiences, skill development, and networking opportunities but also for helping industries lower recruitment costs, access affordable labor, and foster relationships with academic institutions while training future talent [10].

The Stable matching theory, a key concept in mathematics and economics, plays an important role in solving preference-based matching problems in recruitment. This theory, recognized through the Nobel Prize awarded to Roth and Shapley in 2012, addresses how to pair two groups [11]. In this research, the Gale-Shapley algorithm is applied to match employers and interns, systematically modeling recruitment as a preference-driven process that reduces dissatisfaction and turnover [12]. This method is chosen over others because it offers a systematic and robust solution to complex, preference-based matching problems [13]. Unlike other methods, such as random matching or simple ranking, the Gale-Shapley algorithm accounts for the nuanced preferences of both sides, ensuring that each match is stable and less likely to be disrupted by conflicting interests [14].

Our research integrates the Gale-Shapley algorithm with NSGA-III, a Multi-Objective Evolutionary Algorithm (MOEA), to optimize job matching by handling high-dimensional problems better than NSGA-II [15]. NSGA-III uses non-dominated sorting to rank solutions, ensuring optimal trade-offs between employer and intern preferences, while maintaining diversity through reference point association [16]. This approach effectively addresses conflicting objectives in job matching [17].

1.2 Related work

Recent studies have focused on improving recruitment and job-matching through algorithmic solutions. Traditional methods, like ranking and random matching, simplify the process but often overlook the complex needs of both employers and interns, leading to mismatches and dissatisfaction. As a result, research has shifted toward addressing these complexities for better recruitment outcomes.

Yang, H. applied the stable matching algorithm to optimize resource allocation in the decentralized AM sharing economy, showing its superiority over MILP and FCFS in balancing demand-supply scenarios [18]. Yang, D. also explored optimization through a multi-objective model for the flexible job shop scheduling problem (FJSP), minimizing the makespan and energy consumption [19]. The comparison between NSGA-II and MOEA/D solvers demonstrated that NSGA-II provided better real-world solutions.

In the field of internship and job matching, Sawadsitang et al. developed an interview matching framework to optimize internship allocations, validated with real and synthetic data [20]. Zakrzewska proposed a modified Gale–Shapley algorithm to improve the assignment process of Polish pupils to schools, enhancing fairness and allocation efficiency [21]. Building on these frameworks, Ibrahim et al. and Soni explored advanced algorithms to refine matching processes [7, 22]. Ibrahim’s research employed fuzzy logic for internship placement, while Soni focused on AI’s role in recruitment, emphasizing fairness and efficiency. These studies provided key insights into improving placement processes and addressing biases in matching systems [7, 22].

Elgammal streamlined job-hunting by automating resume screening and job recommendations, reducing costs and enhancing satisfaction [23]. Meanwhile, Huang et al. applied the Gale–Shapley algorithm to allocate healthcare resources to the elderly, demonstrating its effectiveness in real-world stable matching scenarios [24]. Mendoza discussed challenges in distinguishing required versus desired skills in recruitment [25]. Yue Wu et al. analyzed modifications to the Gale-Shapley algorithm to address imbalances in residency matching, ensuring stable matches and enhancing hiring stability [26].

Ugale et al solved a problem related to recommending appropriate jobs to job-seekers by matching semi-structured resumes with job descriptions [27]. The performance of their approach was compared to six other models (Table 1), revealing that efficiency increased by understanding each algorithm’s strengths and weaknesses and combining the use of two or more algorithms in parallel in one mode.

Table 1: Outcomes comparison with different models [27].

Model	Word n-gram	BOW	TF-IDF	Bag of Means	Doc2Vec	CNN	Siamese adoption of CNN
Accuracy on test A	58.24	56.92	60.46	62.34	65.24	73.31	81.34
Accuracy on test B	59.01	57.06	61.23	63.92	67.24	74.68	83.19

Pudasaini et al. used word2vec for semantic analysis and the Gale-Shapley algorithm for stable matching between candidates and employers [28]. Similarly, Aziz et al. addressed stable matchings with distributional constraints in a summer internship program, using a Mixed Integer Linear Program (MILP) to find maximum-size matchings [29]. Masood et al. focused on optimizing job scheduling across multiple employers by applying dispatching rules [30]. Building on this, He et al. enhanced the NSGA-III algorithm by improving population diversity and incorporating adaptive local search strategies for better human resource management outcomes [31].

Table 2: Summary of relevant literature according to the applied methods and approaches.

Model	Problems	Reference
GSA	Resource allocation in decentralized systems	H.Yang, 2021
GSA	Elderly misplacement in care facilities	L.Huang, 2024
Modified GSA	Unfair student-school assignments	Zakrzewska, 2024
Modified GSA	Matching with unequal group sizes	Mendoza, 2022
Stable matching model	High energy use in operations	D.Yang, 2020
Profile matching model	Students mismatched to internships	N.Ibrahim, 2021
Resume-job matching model	Unstructured resumes hinder matching	Ugale, 2025
Job matching model	Irrelevant job recommendations	Elgammal, 2021
Interview matching framework	Unbalanced internship distributions	Sawadsitang, 2022
AI-powered recruitment system	Lack of clarity in AI hiring	V.Soni, 2024
Word2vec Model	Hard to spot right candidates	Pudasaini, 2022
Graduates’ job matching	Matching issues in complex systems	H. Aziz, 2024
NSGA-III algorithm	Conflicting multi-objective tradeoffs	Y.He, 2023
D1rules model	Inefficient job-machine scheduling	A.Masood, 2021

1.3 Key contributions

The intern-employer matching process is facing several key challenges, including skill mismatches, differing preferences, and unstable placements. Employers seek specific competencies, while interns prioritize career growth and work environments, making alignment difficult. Ensuring long-term stability is another issue, as initial compatibility doesn’t always lead to lasting success. To address these problems, the study focuses on three questions:

What are the essential factors for a successful intern-employer matching process?
How can a strategic approach be applied to consider the preferences of both employers and interns while ensuring optimal and stable matches?
How can a strategic approach be applied to generate a set of optimal intern-employer matches?

The key factors shaping the matching process include skill requirements, career goals, and work environment. Through a review of research papers, we identified additional factors like internship duration and compensation, which are incorporated into the matching model to improve compatibility and alignment. These factors help define the foundation for a balanced and effective matching process.

Based on these factors, the problem is framed within the stable matching model. Employers and interns are assigned preferences, and the goal is to find a stable match that satisfies both parties’ objectives. This approach ensures that the matching process reflects the priorities and expectations of both sides.

For efficient multi-objective optimization, we use NSGA-III to enhance match quality across multiple objectives. The Gale-Shapley algorithm, as analyzed by Yue Wu et al., ensures stable matches in residency programs by aligning individual preferences [26].

Our research contributes to the field of intern recruitment through the creative and flexible use of NSGA-III and Stable matching theory (SMT).These key contributions are:

Enhance Intern-Employer Matching Process: Our study promotes a balanced and efficient matching system by considering both interns’ aspirations and employers’ requirements in a structured manner.
Ensure Stability and High-Quality Matches: By incorporating 3 models inspired from other studies, we created a structured matching method that enhances fairness and reliability, creating an optimized recruitment system that consistently delivers high-quality matches.
Develop an Optimization Approach for Multi-Objective Recruitment: Our models allow for balancing multiple objectives, such as employer requirements and intern preferences, improving allocation efficiency and recruitment outcomes.

Through these contributions, our research aims to collectively enhance the efficiency, fairness, and adaptability of intern recruitment processes.

Problem definition.

The NSGA-III Based Recruitment Efficiency (NSERE) problem addresses inefficiencies in intern recruitment, such as time waste, mismatches, and reduced productivity. The two parties in NSERE are as follows:

The list of interns is denoted by I = {i1, .. ,iX}, with ia is the intern at the ath position 0 < a X | X ∈ N⁺.
The list of employers is represented as E = {e1, .. ,eY} where ej is the employer at the jth position 0 < j Y | Y ∈ N⁺.

Let:

P be the preference list for intern, the set of employers that ia finds acceptable.
Q be the preference list for employer, the set of intern that ej find acceptable.

Determining characteristics and requirements is crucial to the process of matching employers with interns. Each ej (0j Y) includes a list of employers requirements while an intern ia (0aX) looks for an employer based on their own criteria. Defining that if ia I finding at most m employers ej E acceptable if ej belongs to P, and employer acceptability follows the same principle with Q.

A matching M(ia, ej) in NSERE is acceptable if each intern ia can prefer at most ne employers, and each employer ej can match with at most ni intern. The following requirements of best stable match M have to be covered such that:

Every intern ia is assigned to several employers, more than one employer ej in matching M, and an employer ej can be suggested for numerous interns.
We define M(ia, ej) only if ia and ej formed a match in M (i, e M ). There are no blocking pairs(ia, ej) in M where ia would prefer ej over ej, or ej would prefer i a over ia

The matching process adheres to specific constraints, as detailed in the tables below. Table 3 presents a dataset featuring information on three interns i1, i2, i3 and four employers e1, e2, e3,e4, along with their corresponding characteristics and requirements.

Table 3: Example dataset of intern’s characteristics and employer’s requirements

Interns				Employers
Interns				Employers					No.	i1	i2	i3	No.	e1	e2	e3	e4
GPA	3	3.5	4	GPA	3	4	3.5	2
Working hours (per week)	15	30	20	Working hours (per week)	≥ 10	≥ 35	≥ 25	≥ 15
Expected salary ($)	1300	1700	1300	Salary ($)	1700	2000	1600	1400

The input for NSERE in both algorithms consists of interns I = {i1, .. ,iX}, and employers E = {e1, .. ,eY}, including their attributes and mutual preferences. Employers specify hiring criteria, while interns have their own selection preferences, derived from relevant literature [32, 33].

For each employer jth, characteristics are defined as EjAB, where AB indicates the type of requirement, such as:

Resume requirements EjR: Includes GPA range a,b, Entrance Exam Scores 0-10, and Recommendation Letters.
Personality alignment requirement EjPA: Based on MBTI compatibility with organizational culture and team dynamics.
Working hours requirements EjWH: Specifies the minimum required working hours.
Duration requirements EjD: Defines the expected internship duration in months.

In contrast, the characteristics of the ath intern are defined as IaAB, where AB denotes specific attributes such as company prestige (CP), work environment (WE), basic salary (BS), and geographical location (GL). Intern preferences include:

Company prestige IaCP: Preference for firms rated 1–5 by Reputation Score (RS), Industry Recognition (IR), and Employee Reviews (ER), i.e., CP = RS, IR, ER.
Work environment IaWE: Rated 1–5, considering Colleague Support (CS), Company Benefits (CB), and Job Security (JS), i.e., WE = CS, CB, JS.
Basic salary IaBS: Minimum expected salary in USD.
Geographical location IaGL: Maximum preferred commute distance, in kilometers.

Other intern features include resume IaR, personality alignment IaPA, work hours IaWH, and internship duration IaD. Employer attributes include EjCP, EjWE, EjBSand EjGL.

Table 4: Characteristics of employers and interns

Agents	Employers	Interns
Characteristics	Resume requirements EjR	Company prestige requirements IaCP
	Personality alignment requirements EjPA	Basic salary requirements IaBS
	Work hours requirements EjWH	Geographical location requirements IaGL
	Duration requirements EjD	Work environment requirements IaWE
	Resume IaR	Company prestige EjCP
	Personality alignment IaPA	Basic salary EjBS
	Work hours availability IaWH	Geographical location EjGL
	Duration IaD	Work environment EjWE

The NSERE model tackles mismatches in intern-employer pairing through a multi-objective, stable matching approach. It balances the differing priorities of both sides—interns consider factors like EjCP, EjBS, EjGL, and EjWE, while employers evaluate IaR, IaPA, IaWH and IaD. By applying weighted preferences, constraint satisfaction, and stability checks, the model ensures optimal, mutually beneficial matches, recruitment efficiency.

Figure 3: Flow diagram modeling our approach.

The flowchart outlines the NSERE matching process, beginning with preference lists and using NSGA-III to optimize matches based on skills, preferences, and job criteria. It applies genetic operations and uses Gale-Shapley to form stable, conflict-free pairings.

Methods

3.1 Existing model

In defining the model for optimizing employer-intern matching, several studies influenced our approach to structuring how inputs flow into final pairings. More specifically, Lyu [34] proposed a Stochastic Multi-Objective Optimization Framework (SMOOF) that balances different stakeholders’ priorities. This model incorporates randomness into the optimization process, allowing exploration of multiple feasible solutions.
The mathematical formulation of SMOOF can be interpreted as following:

(S0)maxx(ω ){Eω ∼Ψ[f1(x(ω),ω)],Eω ∼Ψ[f2(x(ω),ω)],…Eω ∼Ψ[fk(x(ω),ω)]} (1)

Where ω denotes a supply-demand scenario drawn from distribution Ψ, and x(ω) the matching solution in scenario ω. The multiple performance metrics are denoted by fk(·), for k = 1, 2,… ,k. The set x(ω) is a convex feasible region associated with the scenario realization , and the maximization is over a vector of performance metrics. By solving this formulation, we balance diverse objectives under uncertainty, making it ideal for real-world matching. Given this insight, our approach extends Stable matching theory with NSGA-III to ensure stable, high-quality employer-intern pairings.

3.2 Model for NSERE

Based on the existing models above and established criteria to address the NSERE, three specialized models were developed, each targeting a key dimension of intern-employer matching:

(i) IECM (Intern-Employer Compatibility Model): Evaluate compatibility based on factors such as EjCP with IaCP, EjBS with IaBS, IaR with EjR, and IaWH and EjWH.

(ii) OSCM (Overall Similarity Calculation Model): Computes mutual similarity scores using weighted preferences and requirements for a pair of interns and employers to evaluate match quality.

(iii) FPEM (Fitness and Payoff Evaluation Model): Assesses overall matching fitness and satisfaction across all pairs, ensuring global optimization and match effectiveness

3.2.1 Intern-Employer Compatibility Model (IECM)

IECM analyzes the similarity between interns Ia 0 < a X | X ∈ N⁺ and employers Ej 0 < j Y | Y ∈ N⁺ based on their attributes and requirements. Similarity is calculated by comparing provided and requested values using specific formulas.

For interns’ characteristic

Regarding resume matching, if the intern’s qualifications align with employer’s requirements.

S(IaR,EjR) = i=13.Wi. Fi (2)

Where W_irepresents the normalized weights for GPA, exam score, recommendation letters. F_i ∈ [0.1] denotes the normalized satisfaction score for each respective criterion. Companies evaluate intern personality alignment with organizational culture using MBTI, scoring each of four dimensions where m_i is the dimension’s match score.

S(IaPA,EjPA) = 14i=14mi (3)

Working hours and internship duration similarity depends on intern availability versus employer requirements, scoring 1 for a perfect match and less for differences (hours > 0, duration > 1 month).

S(IaWH,EjWH) = min (1,IWHaEWHj) (4)

and

S(IaD,EjD) = min (1,IDaEDj) (5)

For employers’ characteristics:

We considered binary 0 or 1, comparability for unique attributes like work environment and company prestige, specifically:

S(IaWE,EjWE) = 1 if IaWE=EjWE (5)

S(IaWE,EjWE) = 0 if IaWEEjWE (6)

and

S(IaCP,EjCP) = 1 if IaCP=EjCP (6)S(IaCP,EjCP) = 0 if IaCP EjCP (7)

The similarity value of basic salary is denoted as follows:

S(EjBS,IaBS) = EBSjIBSa if EjBS < IaBS (7)

S(EjBS,IaBS) = 1 if EjBS >= IaBS (8)

Lastly, we calculate the similarity of geographical location between employers and interns requirement:

S(EjGL,IaGL ) =ED AD if ED < AD (8)

S(EjGL,IaGL ) =1 if ED > AD (9)

In which, ED is expected distance from interns (from IaGL to the intern’s residence), while AD represents the actual distance from the intern’s settlement to the company geographical location EjGL.

3.2.2 Overall Similarity Calculation Model (OSCM)

OSCM evaluates intern-employer suitability through bidirectional weighted similarity scores:

Interns to Employers Similarity IaI={I1, .. ,IX} and employer EjE={E1, .. ,EY}

OS(Ia,Ej)=a=1Xj=1Yk=14WkIa. Sk(Iak,Ejk) (10)

Employer to Intern Similarity:

OS(Ej, Ia)=a=1Xj=1Yk=14WkEj. Sk(Ejk, Iak) (11)

Where:

WkIa, WkEj: The weight assigned to the 𝑘 k-th attribute from the intern’s and employer’s perspectives, respectively.

Iak,Ejk: The k-th attribute values of intern Ia and employer Ej.

Sk(x, y): A similarity function that measures the compatibility between two corresponding attribute values

3.2.3 Fitness and Payoff Evaluation Model (FPEM)

FPEM optimizes intern-employer matching by assessing compatibility at individual and group levels, ensuring each intern iaI pairs with at least one suitable employer ejE and vice versa, based on mutual criteria. The total fitness function sums similarity scores for all matched pairs M(ia, ej,):

f=a=1,j=1COS(ej,ia)+OS(ia,ej) (12)

The diagram below illustrates the sequential integration of three models in our matching system. First, the IECM calculates basic compatibility scores by comparing intern characteristics with employer requirements across key dimensions like resume quality, personality traits, working hours, and salary expectations. These raw compatibility metrics then flow into the OSCM, where they are weighted according to both parties’ priorities – employers might emphasize resume quality while interns prioritize salary and company prestige. Finally, the FPEM aggregates these weighted scores to evaluate the overall quality of potential matches across all possible pairings.

Figure 4: Illustration of connection between 3 models

A novel employer-intern matching model would be introduced by integrating Stable matching theory with NSGA-III and the Gale-Shapley algorithm. Unlike conventional approaches centering on preference rankings, our model treats employers and interns as strategic agents, enabling multi-criteria decision-making. NSGA-III facilitates efficient exploration of large solution spaces, balancing trade-offs among competing objectives to yield high-quality matches. This hybrid approach enhances scalability and realism in recruitment, offering a computationally efficient framework for optimized, strategic pairings.

3.3 Algorithm

An NP‑hard problem is one to which every decision problem LNP can be reduced in polynomial time, making it at least as hard as the hardest problems in NP [35]. The NSERE matching problem is considered a NP-hard problem by this definition. With N interns and employers, the number of potential assignments grows exponentially with worst case time complexity O(N!), so verifying a stable match requires exponential effort, and for any NP decision problem L and input x, we can in polynomial time build an NSERE instance f(x) such that:

xLf(x) admits a stable matching

i.e. L NP, LPNSERE hence, NSERE is an NP-hard problem

Our approach to this NP-hard problem is combining the Gale-Shapley algorithm ensures stable matchings between interns and employers, while NSGA-III mitigates proposer-optimal bias by generating diverse preferences.

The Gale-Shapley algorithm addresses the challenge of matching interns with employers by ensuring stable pairings. It relies on two sets of preference lists: P representing the preferences of the interns and Q representing the preferences of the employers, both defined in the Problem definition section. A matching is stable when no unmatched intern-employer pair (Ia, Ej) prefers each other over their assigned partners. With time complexity O(N2),the algorithm guarantees feasible computation even in large-scale recruitment scenarios. Interns propose to their top-choice employers, and employers tentatively accept the most preferred candidates while rejecting others. This process continues until stable matches are formed.

While Gale-Shapley effectively ensured stable NSERE matchings, its proposer-optimal bias favored initial preferences. Thus, NSGA-III, an MOEA, was integrated to generate diverse, randomized preference lists mitigating this bias. Gale-Shapley then produced stable matchings. To achieve this, NSGA-III encoded matchings as chromosomes Cr = {cr1, .. ,crn}, linking interns I = {i1, .. ,iX} and employers E = {e1, .. ,eY}. The fitness function (11) f(cr) evaluates these matchings based on factors like resume quality, working hours, and salary. NSGA-III used reference-point-based non-dominated sorting to ensure diverse, well-distributed pairings with complexity O(NlogN, while Gale-Shapley’s complexity was ON2, yielding a combined cost of O(Nlog N+ N2). Key parameters like population size, objectives, edge weights, mutation, and crossover rates, were tuned to enhance diversity and optimize matchings.

In the employer-intern matching problem, a chromosome (cr) represents a candidate solution encoding potential intern-employer pairs. Each chromosome is a vector where elements correspond to specific pairings. The size of cr, equals the total number of possible pairs M(ia, ej), the payoff values for each pair are calculated using equation (11), measuring mutual compatibility and satisfaction.

Figure 5: Visualialter, restrict, or revoke access without player consentzation of chromosome

The fitness function is a key part of the algorithm, evaluating how effective each chromosome is as a potential matching solution. After every mutation stage, chromosomes Cr create offspring O in optimum pairing. Each offspring’s fitness level f(O) can be expressed as equation (11). The top-performing offspring chromosomes, based on f(O), are selected as parents P for the subsequent mutation stage. This iterative assessment ensures each chromosome cri obtains optimal fitness f(cri) in relation to the characteristics and the requirements of both agents.

Figure 6: The process of selecting pairs of chromosomes.

The below diagram displays the process flow of the mixed algorithms NSGA-III and Gale-Shapley: alter, restrict, or revoke access without player consent

Figure 7: The process flow of the algorithm.

The figure illustrates the integration of NSGA-III and Gale-Shapley for solving the NSERE problem. Intern data I={i1,….,ix} and employer data E={e1,….,ey} are input, and NSGA-III generates preference lists through information exchange, mutation of ixand ey, and fitness evaluation function f. Then Gale-Shapley uses these lists to form stable matches. These matches are evaluated against additional quality criteria, if they fail, the process loops; otherwise, stable matches are output, ensuring efficient and balanced pairing.

The Pseudo code illustrates a hybrid approach integrating NSGA-III with the Gale-Shapley algorithm to address multi-objective stable matching in the NSERE model. NSGA-III identifies high-quality matchings by optimizing multiple objectives. The Gale-Shapley procedure subsequently ensures stability by aligning outcomes with individual preference rankings.

Figure 8: Pseudo code for applying NSGA-III and Gale-Shapley algorithms

NSGA-III explores a diverse solution space through crossover, mutation, and selection guided by performance metrics. The resulting matchings inform the construction of preference lists. These are refined into stable, optimized pairings using the Gale-Shapley algorithm.

Result

This section shows a comprehensive review of computational experiments to ensure the efficiency and availability of the applied algorithms and functions. The server configuration used to address the problem includes the following technical specifications: Windows 11 operating system powered by a 10th Gen Intel(R) Core(TM) i5-7200U CPU @ 2.50GHz, 8GB RAM, 256GB SSD Storage, and GPU NVIDIA GTX 2050.

Table 5: The table of experiment parameters.

Experiment Parameters	Number of generation	Number of characteristics	Edge weight	Mutation rate	Crossover rate
Value	2000	8	[1,10]	0.01	0.8

Table 5 above summarizes the experimental parameters, which include a population size of 1000 interns and 1000 employers, evolved over 2000 generations. Each agent is assigned 4 characteristics, which pay different attention to each characteristic on a 10-point scale as the edge weight represents. The NSGA-III algorithm was configured with a mutation rate of 0.01 and a crossover rate of 0.8 to ensure a diverse exploration of the solution space.

In this section, we are proposing a sample data set of two groups: group of 1000 interns I={i1, .. , i1000} and group of 1000 employers E={e1, .. , e1000}, including a part of the dataset collected from Kaggle website with similarity to the characters mentioned in this paper.The table 6 below summarizes two individuals in each group. The table presents each individual’s properties (p), their requirements (req) from the opposite side, and the weight (w) of each requirement (1–10) based on preference. This setup, based on the article by [36], helps standardize compatibility and prioritize key preferences for fair and efficient matching.

Table 6: The sample dataset of interns and employers

	i₁	i₂	e₁	e₂
I^R	15.03 – 4 – 24.97	95.66 – 1 – 7.37	12.28 – 4 – 93.87	75.30 – 9 – 94.8
I^PA	63.21- 4 – 68.9	44.26 – 4 – 31.18	2.40:53.25 – 1 – 17.1	55.69 – 8 – 19.61
I^WH	60.61 – 2 – 65.04	69.13 – 1 – 87.67	20.31 – 4 – 53.47	92.75 – 3 – 35.87
I^D	35.82:59.70 – 9 – 15	76.81 – 2 – 17.51	28.78 – 7 – 62.19	21.2 – 9 – 64.71
E^CP	75.86 – 4 – 16.17	41.91:80.08 – 6 – 38.8	3.36 – 9 – 4.6	39.69:75.21 – 2 – 86
E^BS	43.52 – 8 – 29.92	4.00 – 4 – 32.44	96.91 – 7-18.35	39.41 – 3 – 20.87
E^GL	75.14 – 1 – 76.36	72.83 – 4 – 58.76	28.52 – 7 – 24.56	20.03:56.87 – 3 – 47.19
E^WE	46.89 – 4 – 95.14	27.16:66.26 – 3 – 97.65	80.72 – 6 – 83.57	57.62 – 5 -86.08

Both employers and interns are assessed in these samples based on their individual weights and requirements. While employers consider resume I^R, personal alignment I^PA, work hours I^WHand duration I^D, interns prioritize company prestige E^CP, basic salary E^BS, geographical location E^GL and work environment E^WE

Figure 9: Sample of matching result

Figure 9 illustrates a sample result showing the matches between interns and employers, represented as ix and ey, where x and y are the index of the interns and employers respectively with their satisfaction value.

Table 7: Comparison experiment including fitness values and runtime across different algorithms on the data set of 2000 individuals

	NSGA III	eMOEA	PESA2	VEGA
1	171549.7/5.044	168769.3/5.076	172950/5.05	165070.2/5.043
2	171797.2/5.042	168451.5/5.003	172815.1/5.023	165179.8/5.087
3	170970.5/5.027	168501.9/5.011	172703.9/5.004	166214/5.035
4	171533/5.035	169575.6/5.001	172686/5.026	165898/5.032
5	171300.3/5.022	169060/5	173084.5/5.017	165528.8/5.036
6	172299.5/5.01	169019.7/5.009	172705.6/5.028	165827.1/5.052
7	171790.2/5.013	168959.1/5.004	173110.3/5.011	165613.7/5.06
8	173226.4/5	168682.1/5	172725.2/5.011	165653.2/5.017
9	172605.3/5.026	168598.5/5	173432.4/5.005	167150.8/5.045
10	172142.35.008	168790.1/5	171833.1/5.005	165771.4/5.038

Table 7 summarizes an experiment on a dataset of 2000 individuals, comparing four algorithms for multi-objective optimization: eMOEA, PESA2, VEGA, and NSGA-III. Each algorithm has unique strengths and approaches. eMOEA uses tabu-based rules to guide solution exploration [37]. PESA2 employs grid-based fitness assignment for environmental selection [38]. VEGA integrates virus populations and infection operators to avoid premature convergence and enhance solution accuracy [39]. NSGA-III excels in many-objective problems, leveraging adaptive reference points to maintain diversity [40]. While NSGA-III excels in complex optimization, comparative benchmarking is essential to rigorously evaluate its robustness and delineate its strengths and limitations in the intern–employer matching context.

Each cell in table 7 contains a fitness value indicating optimization quality, along with the corresponding runtime. The results show generally stable execution times, while fitness scores exhibit some variability across runs, likely due to stochastic elements in the algorithms.

Iteration 1

c. Iteration 3

Iteration 2

d. Iteration 4

Figure 10: A comparison of runtime (in seconds) across four generic algorithms of 2000 individuals

The runtime performance of the four algorithms over the first four iterations is illustrated in Figure 10. Each subfigure shows actual execution times under the same conditions. The data reveals consistent runtimes around 5 seconds, with minimal variation among algorithms and iterations, reflecting stable computational performance.

Fitness score of VEGA algorithm

Fitness score of PESA2 algorithm

Fitness score of NSGAIII algorithm

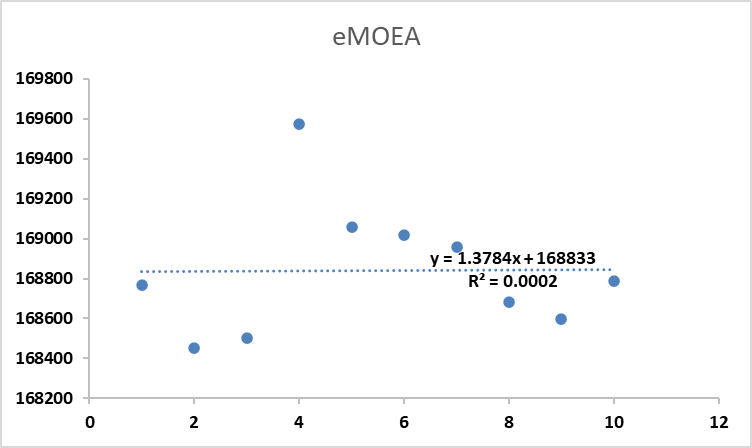
Fitness score of eMOEA algorithm

Figure 11: Comparison of fitness score across four generic algorithms after several execution times.

The variation in fitness scores across the 10 runs for each algorithm is visualized in Figure 11. Each chart includes data points, a linear trendline, and an R² value, highlighting the degree of consistency in optimization performance. These visualizations offer insights into the internal behavior of each algorithm across repeated executions, beyond just average results.

Discussion

While PESA2 achieved the highest mean fitness-to-time ratio (34.438) with a standard deviation () of 121.8, NSGA-III, with a comparable mean (34.230) and slightly lower variability ( = 121.6), emerges as the preferred algorithm due to its faster average runtime, which enhances its suitability for larger datasets or more complex problems by consistently delivering high-quality results more efficiently; in contrast, eMOEA’s lower mean (33.699) and higher variance ( = 194.3) reflect its limited global exploration, and VEGA’s weakest performance (mean = 32.867, = 200.7) stems from its simplistic, non-elitist selection mechanism, ultimately reinforcing NSGA-III’s balanced advantage in both efficiency and reliability.

This study improves the intern-employer matching process by integrating NSGA-III with the Gale-Shapley algorithm, addressing limitations in prior works. While Sawadsitang et al. focused on structured interview-based allocation without multi-objective optimization, achieving a runtime of 12.5 seconds for 100 interns and 20 organizations [20], our approach combines preference diversity and stability for more balanced results. Using a dataset of 1000 interns and 1000 employers, it achieves comparable or better matching quality with an average runtime of only 5.008 seconds, demonstrating superior scalability and efficiency.

While our proposed model enhances recruitment efficiency by combining NSGA-III and Gale-Shapley algorithms, several limitations remain. The model assumes rational preferences from both employers and interns, which may not reflect real-world uncertainties. Additionally, our current dataset and simulations are limited in size and diversity, so the computational complexity of multi-objective optimization could become a bottleneck in large-scale applications. Future research could explore incorporating dynamic preferences, applying machine learning to predict or infer rankings, and testing the model with real-world data to further validate and refine its effectiveness.

Conclusion

Internship recruitment faces challenges in effectively matching employers with interns, leading to missed opportunities for highly skilled interns and underutilized talent, which in turn hampers organizational efficiency and growth. In this paper, we applied the NSGA-III algorithm to generate two unordered sets of individuals with equal matching opportunities, used the Gale-Shapley algorithm to pair them into stable matches, and compared the values of each match to determine the final result. Our study proposed a mathematical model that effectively addresses complex many-to-many pairing problems, demonstrated improved matching quality compared to traditional methods and ultimately achieved a stable matching solution. The NSGA-III algorithm achieves high fitness values, especially with more crossover generations. Combined with the Gale-Shapley algorithm, it ensures optimal pairing efficiency but requires longer execution times for large populations and complex problems. In general, this is crucial for bringing interns and employers together within a labor market that is undergoing major upheavals, making it challenging for interns to get internships.

REFERENCES

P. Kurniawan and N. Susanto, “The Effect of Job Stress, Job Satisfaction and Emotional Intelligence on Turnover Intention,” Int. J. Sci. Technol. Manag., vol. 4, no. 2, pp. 358–365, 2023, DOI: 10.46729/ijstm.v4i2.763.
P. Mahesh, “Understanding the development of soft skills in professional students of engineering colleges of rural area of Guntur district,” Alford Council Int. English Lit. J., vol. 7, no. 2, pp. 10–29, Jun. 2024, DOI: 10.37854/ACIELJ.2024.7202.
T. Q. Tran, N. B. T. Vu, and H. V. Vu, “Does job mismatch affect wage earnings among business and management graduates in Vietnam?,” Research in International Business and Finance, vol. 65, p. 101982, 2023, DOI: 10.1016/j.ribaf.2023.101982.
A. Uz-Zaman and M. A. M. Khan, “Minimum wage impact on RMG sector of Bangladesh: Prospects, opportunities and challenges of new payout structure,” International Journal of Business and Economics Research, vol. 10, no. 1, pp. 8–20, 2021, DOI: 10.11648/j.ijber.20211001.12.
Y. Rivaldo and S. D. Nabella, “Employee performance: Education, training, experience and work discipline,” 2023, DOI: 10.47750/QAS/24.193.20.
S. Hugar and S. Bhat, “Challenges faced by human resource recruiters in post selection of freshers in IT companies,” 2021, DOI: 10.17605/OSF.IO/C5VTU.
N. Ibrahim, H. M. Hanum, Z. Abu Bakar, and N. A. S. Abdullah, “Student-industry matching for internship placement,” in Proc. 2021 Fifth Int. Conf. Inf. Retr. Knowl. Manag. (CAMP), 2021, pp. 122–126, DOI: 10.1109/CAMP51653.2021.9498088.
M. K. Bairwa and R. Kumari, “Perception and expectations of interns: A study on internship in hospitality education,” in Hospitality and Tourism Emerging Practices in Human Resource Management, 2021.
C. Neves, M. Nogueira, and S. Gomes, “Looking to the future: Grasping students’ expectations regarding employers’ attractiveness,” in EDULEARN Proceedings, vol. 1, pp. 7833–7839, 2021, DOI: 10.21125/edulearn.2021.1597.
Y. Hou, “Avoiding the gap of college students’ internship expectations and perceptions—A case study in Taiwan,” Open J. Nurs., vol. 8, no. 8, pp. 531–551, 2018, DOI: 10.4236/ojn.2018.88040.
A. E. Roth and L. S. Shapley, “The theory of stable allocations and the practice of market design,” American Economic Review, vol. 102, no. 4, pp. 1660-1682, 2012, DOI: 10.1257/AER.102.4.1660.
D. M. Edmonds, O. Zayts-Spence, Z. Fortune, and J. S. Y. Fung, “Graduates’ perceptions and employers’ expectations: Essential skills in Hong Kong workplaces during the COVID-19 pandemic and beyond,” Industry and Higher Education, vol. 38, no. 1, pp. 23–34, 2024, DOI: 10.1177/09504222231224087.
N. T. N. Ha and E. Dakich, “Student internship experiences: areas for improvement and student choices of internship practices,” Education + Training, vol. 64, no. 4, pp. 516–532, 2022, DOI: 10.1108/ET-09-2021-0337.
I. Ashlagi, J. Chen, M. Roghani, and A. Saberi, “Stable Matching with Interviews,” Proceedings of the 16th Innovations in Theoretical Computer Science Conference (ITCS 2025), vol. 325, pp. 12:1–12:20, 2025, DOI: 10.4230/LIPIcs.ITCS.2025.12.
H. Lee, H. Lee, S. Jung, and J. Kim, “Stable marriage matching for traffic-aware space-air-ground integrated networks: A Gale-Shapley algorithmic approach,” in Proc. 2022 Int. Conf. Inf. Netw. (ICOIN), pp. 474–477, 2022, DOI: 10.1109/ICOIN53446.2022.9687261.
Opris, A., Dang, D. C., Neumann, F., and Sudholt, D., 2024. “Runtime Analyses of NSGA-III on Many-Objective Problems”. In Proceedings of the Genetic and Evolutionary Computation Conference Companion (GECCO ’24 Companion), July 2024. DOI: 10.1145/3638529.3654218.
S. Wietheger and B. Doerr, “A mathematical runtime analysis of the non-dominated sorting genetic algorithm III (NSGA-III),” in Proc. 32nd Int. Joint Conf. Artif. Intell. (IJCAI), Macao, Macau SAR China, Aug. 2023.
H. Yang, R. Chen, and S. Kumara, “Stable matching of customers and manufacturers for sharing economy of additive manufacturing,” J. Manuf. Syst., vol. 61, pp. 1–12, Oct. 2021, DOI: 10.1016/j.jmsy.2021.09.013.
D. Yang, X. Zhou, Z. Yang, Q. Jiang, and W. Feng, “Multi-objective optimization model for flexible job shop scheduling problem considering transportation constraints: A comparative study,” in 2020 IEEE Congress on Evolutionary Computation (CEC), 2020, pp. 1–8, DOI: 10.1109/CEC48606.2020.9185653.
S. Sawadsitang, D. Niyato, W. Mahanan, J. Thanyaphongphat, and R. Kaewpuang, “Intern-organization interview matching framework: An optimization approach,” in 2022 37th International Technical Conference on Circuits/Systems, Computers and Communications (ITC-CSCC), 2022, pp. 947–950, DOI: 10.1109/ITC-CSCC55581.2022.9895049.
A. Zakrzewska, “A modification of the Gale-Shapley algorithm used to assign Polish pupils to schools,” Studia Informatica Syst. Inf. Technol., vol. 30, no. 1, pp. 97–104, 2024, DOI: 10.34739/si.2024.30.07.
V. Soni, “AI in job matching and recruitment: Analyzing the efficiency and equity of automated hiring processes,” in 2024 International Conference on Knowledge Engineering and Communication Systems (ICKECS), 2024, pp. 1–5, DOI: 10.1109/ICKECS61492.2024.10617325.
Z. Elgammal, A. Barmu, H. Hassan, K. Elgammal, T. Özyer, and R. Alhajj, “Matching applicants with positions for better allocation of employees in the job market,” in 2021 22nd International Arab Conference on Information Technology (ACIT), 2021, pp. 1–5, DOI: 10.1109/ACIT53391.2021.9677374.
M. Hu, W. Zhu, and X. Yu, “Application of Gale–Shapley algorithm in optimal matching for healthcare facilities to elderly population: The case of Hangzhou, China,” Applied Economics, vol. 56, no. 10, pp. 913–925, 2024. DOI: 10.1080/00036846.2024.2320175.
A. A. D. Mendoza, L. J. C. Barbosa, D. M. A. Cortez, R. M. Dioses, V. A. Agustin, and R. C. Regala, “Enhancement of Gale-Shapley algorithm with imbalanced sets for hiring and job finding applications,” Indones. J. Electr. Eng. Comput. Sci., vol. 27, no. 2, pp. 954–958, 2022, DOI: 10.11591/ijeecs.v27.i2.pp954-958.
Yue Wu, A. J. H. Brown, and J. E. Moore Jr., “Inefficiencies in residency matching associated with Gale–Shapley algorithms,” Ophthalmology, vol. 130, no. 2, pp. 183–191, Feb. 2023, DOI: 10.1016/j.ophtha.2022.09.017.
A. V. Ugale, “Resume clustering and job description matching,” Int. J. Res. Appl. Sci. Eng. Technol., vol. 13, no. 4, pp. 2881–2887, 2025, DOI: 10.22214/ijraset.2025.68831.
S. Pudasaini, S. Shakya, S. Lamichhane, S. Adhikari, A. Tamang, and S. Adhikari, “Scoring of resume and job description using Word2vec and matching them using Gale–Shapley algorithm,” in Proceedings of the International Conference on Advanced Computing and Intelligent Engineering (ICACIE 2021), 2022, pp. 1–10, DOI: 10.1007/978-981-16-2126-0_55.
H. Aziz, A. Baychkov, and P. Biró, “Cutoff stability under distributional constraints with an application to summer internship matching,” Math. Program., vol. 203, pp. 247–269, 2024, DOI: 10.1007/s10107-022-01917-1.
A. Masood, G. Chen, and M. Zhang, “Feature selection for evolving many-objective job shop scheduling dispatching rules with genetic programming,” in Proc. IEEE Congr. Evol. Comput. (CEC), Kraków, Poland, 2021, pp. 644–651, DOI: 10.1109/CEC45853.2021.9504895.
Y. He, L. Liu, J. Mao, and Z. Liao, “Improved NSGA-III algorithm for solving multi-objective flexible job shop scheduling problem,” in Proc. 7th CAA Int. Conf. Veh. Control Intell. (CVCI), Changsha, China, 2023, pp. 1–6, DOI: 10.1109/CVCI59596.2023.10397364.
M. Fan, J. Chen, Z. Xie, H. Ouyang, S. Li, and L. Gao, “Improved multi-objective differential evolution algorithm based on a decomposition strategy for multi-objective optimization problems,” Sci. Rep., vol. 12, no. 1, 2022, DOI: 10.1038/s41598-022-25440-7.
C. L. Hicklenton, D. W. Hine, A. B. Driver, and N. M. Loi, “How personal values shape job seeker preference: A policy capturing study,” PLoS ONE, vol. 16, no. 7, 2021, DOI: 10.1371/journal.pone.0254646.
G. Lyu, W. C. Cheung, C.-P. Teo, and H. Wang, “Multi-objective stochastic optimization: A case of real-time matching in ride-sourcing markets,” Manuf. Serv. Oper. Manag., 2023, DOI: 10.1287/msom.2020.0247.
Z. Á. Mann, “The Top Eight Misconceptions about NP-Hardness,” Computer, vol. 50, no. 5, pp. 72–75, May 2017, DOI: 10.1109/MC.2017.146.
O. Saidani, L. J. Menzli, A. Ksibi, N. Alturki, and A. S. Alluhaidan, “Predicting student employability through the internship context using gradient boosting models,” IEEE Access, vol. 10, pp. 46472–46489, 2022, DOI: 10.1109/ACCESS.2022.3170421.
K. C. Tan, E. F. Khor, T. H. Lee, and Y. J. Yang, “A tabu-based exploratory evolutionary algorithm for multiobjective optimization,” Artif. Intell. Rev., vol. 19, no. 3, pp. 231–260, May 2003, DOI: 10.1023/A:1022863019997.
M. Li, X. Liu, and K. Wang, “IPESA-II: Improved Pareto envelope-based selection algorithm II,” in Proc. 7th Int. Conf. Simulated Evolution Learn. (SEAL), Lecture Notes in Computer Science, vol. 7811, pp. 143–151, 2013, DOI: 10.1007/978-3-642-37140-0_14.
F. Corno, M. S. Reorda, and G. Squillero, “VEGA: A verification tool based on genetic algorithms,” in Proc. Int. Conf. Comput. Design: VLSI Comput. Process. (ICCD), Austin, TX, USA, Oct. 1998, pp. 321–326, DOI: 10.1109/ICCD.1998.727069.
Y. Yuan, H. Xu, and B. Wang, “An improved NSGA-III procedure for evolutionary many-objective optimization,” in Proc. Genet. Evol. Comput. Conf. (GECCO), Vancouver, BC, Canada, Jul. 2014, pp. 661–668, DOI: 10.1145/2576768.2598342.

Enhancing Recruitment Efficiency: Leveraging Stable Matching Theory with NSGA-III and Gale-Shapley Algorithms for Optimal Employer-Intern Pairing